7 Prinsip Pemuaian dalam Kehidupan Sehari-hari + Gambar, Contoh Soal dan Pembahasan
https://juniorsciences.blogspot.com/2020/08/prinsip-pemuaian-dalam-kehidupan.html
Daftar Materi IPA Terpadu
Advertisement
Baca Juga:
Tahukah kamu, mengapa di siang hari yang panas aspal jalan raya dapat retak? Sambungan rel kereta api harus dibuat renggang? Besi-besi penghubung pada jembatanpun harus dibuat renggang?
Lalu, coba kamu amati bingkai kaca jendela di ruang kelasmu! Adakah bingkai jendela yang melengkung? Tahukah kamu apa sebabnya?
Perinstiwa pada aspal, sambungan rel, dan besi penghubung jembatan tersebut tidak lain karena mengalami pemuaian.Hal itu sangat berkaitan dengan sifat pemuaian dan penyusutan zat. Peristiwa pemuaian dan penyusutan terjadi pada zat padat, zat cair, dan gas.
Berikut akan dibahas penjelasan meneganai pemuaian dan penyusutan pada 3 zat tersebut.
1) Pemuaian Zat Padat
Pemuaian yang terjadi pada benda, sebenarnya terjadi pada seluruh bagian benda tersebut. Namun, untuk mempermudah pemahaman kamu maka pemuaian dibedakan 3 macam, yaitu :
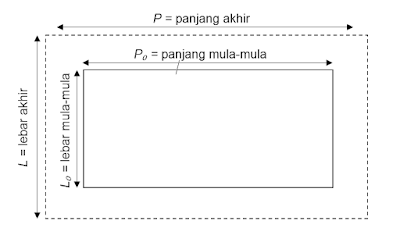
a) Pemuaian Panjang
Pernahkah kamu mengamati kabel jaringan listrik pada pagi hari dan siang hari? Kabel jaringan akan tampak kencang pada pagi hari dan tampak kendor pada siang hari. Kabel tersebut mengalami pemuaian panjang akibat terkena panas sinar matahari.
Untuk menyelidiki pemuaian panjang berbagai jenis zat padat digunakan alat yg bernama musschenbroek.
Pemuaian panjang suatu benda dipengaruhi oleh panjang mula-mula benda, besar kenaikan suhu, dan tergantung dari jenis benda.
Besarnya panjang zat padat untuk setiap kenaikan 1°C pada zat sepanjang 1 m disebut koefisien muai panjang (α). Hubungan antara panjang benda, suhu, dan koefisien muai panjang dinyatakan dengan persamaan berikut.
L = L₀ ( 1 + α . Δt )
Keterangan :
L = Panjang setelah pemanasan atau pendinginan (m) atau (cm)
Lₒ = Panjang awal (m) atau (cm)
α = Koefisien muai panjang ( / °C )
Δt = Kenaikan suhu ( °C )
Berikut adalah tabel koefisien berbagai jenis bahan.
No.
|
Nama Bahan
|
Koefisien Muai Panjang ( / ºC )
|
1.
|
Intan
|
12 x 10⁻⁵
|
2.
|
Kuningan
|
1,9 x 10⁻⁵
|
3.
|
Tembaga
|
1,7 x 10⁻⁵
|
4.
|
Es
|
510 x 10⁻⁵
|
5.
|
Aluminium
|
2,4 x 10⁻⁵
|
6.
|
Baja
|
1,1 x 10⁻⁵
|
7.
|
Platina
|
0,9 x 10⁻⁵
|
8.
|
Kaca
|
0,9 x 10⁻⁵
|
9.
|
Kaca (pyrex)
|
0,3 x 10⁻⁵
|
10.
|
Invar
|
0,1 x 10⁻⁵
|
11.
|
Gafit
|
0,8 x 10⁻⁵
|
12.
|
Emas
|
1,4 x 10⁻⁵
|
13.
|
Perak
|
1,9 x 10⁻⁵
|
14
|
Perunggu
|
1,9 x 10⁻⁵
|
15
|
Berlian
|
0,1 x 10⁻⁵
|
Dibawah ini akan diberikan contoh soal agar lebih mudah untuk dipahami.
Pada suhu 25 °C sebatang kuningan yang panjang 1 m, koefisien muai panjang 1,9 x 10⁻⁵ /°C. Hitunglah panjang kuningan pada suhu 75 °C !
Penyelesaian :
Diketahui :
Lₒ = 1 m = 100 cm
Δt = 75 °C – 25 °C = 50 °C
α = 1,9 x 10⁻⁵ /°C = 0,000019 /°C
Ditanya :
L =...?
Jawab :
L = L₀ ( 1 + α . Δt )
L = 100 ( 1 + 0,000019 x 50 )
L = 100 ( 1,00095 )
L = 100,095 cm
Jadi, panjang kuningan setelah dipanasi adalah 100,095 cm.
b) Pemuaian Luas
Jika yang dipanaskan adalah suatu lempeng atau plat tipis maka plat tersebut akan mengalami pemuaian pada panjang dan lebarnya. Dengan demikian lempeng akan mengalami pemuaian luas atau pemuaian bidang.
Pertambahan luas zat padat untuk setiap kenaikan 1°C pada zat seluas 1 m² disebut koefisien muai luas ( β ).
Hubungan antara luas benda, pertambahan luas suhu, dan koefisien muai luas suatu zat adalah sebagai berikut.
A = A₀ + ΔA
ΔA = A₀ - β . Δt
ΔA = A₀ ( 1 + β . Δt )
Keterangan :
A = Luas akhir (m²)
A₀ = Luas mula-mula ( m² )
ΔA = Pertambahan luas ( m² )
β = Koefisien muai luas zat ( /°C )
Δt = Kenaikan suhu ( °C )
“ Besarnya ( β ) dapat dinyatakan dalam persamaan ( β = 2α ) “
Dibawah ini akan diberikan contoh soal agar lebih mudah untuk dipahami.
Suatu plat aluminium berbentuk persegi dengan panjang sisi 20 cm ( P₀ ) pada suhu 25 °C. Koefisien muai panjang aluminium 2,4 x 10⁻⁵ /°C. Tentukan pertambahan luas plat tersebut jika dipanasi hingga suhu 100 °C !
Penyelesaian :
Diketahui :
P₀ = 20 cm
Δt = 100 °C
α = 2,4 x 10⁻⁵ /°C = 0,000024 /°C
Ditanya :
ΔA =...?
Jawab :
A₀ = P₀ . P₀
= 20 cm x 20 cm
= 400 cm²
β = 2α
= 2 x 0,000024 /°C
= 0,000048 /°C
ΔA = A₀ ( 1 + β . Δ t )
= 400 cm² ( 1 + 0,000048 /°C x 100 °C )
= 1,0048 cm²
Jadi, pertambahan luas plat aluminium tersebut setelah dipanasi adalah 1,0048 cm².
c) Pemuaian Volume
Jika zat padat yang dipanaskan berbentuk bangun ruang, seperti bola, kubus, atau balok, dan sebagainya (dimensi tiga), maka bangun ruang tersebut mengalami pemuaian yang disebut muai volume.
Pada muai volume, pemuaiannya dianggap ke semua arah, yakni bertambahnya panjang, lebar, dan tinggi zat padat tersebut.
Koefisien pemuaian pada pemuaian volume ini disebut koefisien muai volume atau koefisien muai ruang yang diberi lambang ( γ = gamma ). Sehingga berlaku persamaan sebagai berikut.
ΔV = V₀ . γ . Δt
V = V₀ ( 1 + γ . Δt )
Dimana :
γ = 3α atau γ = ( 3/2 ) β
Keterangan :
V = Volume akhir ( mᶟ )
V₀ = Volume mula-mula ( mᶟ )
ΔV = Pertambahan volume ( mᶟ )
γ = Koefisien muai volume ( /°C )
Δt = Kenaikan suhu ( °C )
Dibawah ini akan diberikan contoh soal agar lebih mudah untuk dipahami.
Balok tembaga suhunya 25 °C, dengan volume 65 cmᶟ. Berapakah volume balok apabila suhu dinaikkan menjadi 95 °C ( koefisien muai panjang tembaga 1,7 x 10⁻⁵ /°C ) ?
Penyelesaian :
Diketahui :
V₀ = 65 cmᶟ
t1 = 25 °C
t2 = 95 °C
α = 1,7 x 10⁻⁵ /°C = 0,000017 /°C
γ = 3α = 3 x 0,000017 /°C = 0,000051 /°C
Ditanya :
V =...?
Jawab :
V = V₀ ( 1 + γ . Δt )
V = 65 ( 1 + 0,000051 x ( 95 - 25 ) )
V = 65 ( 1,00364 )
V = 65,2366 cmᶟ
Jadi, volume balok setelah dipanaskan adalah 65,2366 cmᶟ.
2) Pemuaian Zat Cair
Apakah zat cair juga memuai? Pernahkah kamu dikejutkan oleh tumpahnya air ketika sedang memasak air? Mengapa hal itu bisa terjadi?
Pemuaian yang terjadi pada zat cair hanya pemuaian volume. Hal ini disebabkan zat cair selalu menempati bentuk dan isinya.
Pemuaian zat cair setiap benda berbeda-beda bergantung pada suatu besaran yang disebut koefisien muai volume. Semakin besar koefisien muai volumenya, semakin besar pula pemuaiannya.
Pada zat cair tidak melibatkan muai panjang ataupun muai luas, tetapi hanya dikenal muai ruang atau muai volume saja. Semakin tinggi suhu yang diberikan pada zat cair itu maka semakin besar muai volumenya.
Berikut ini adalah tabel dari beberapa koefisien muai volume zat cair.
No.
|
Nama Zat Cair
|
Koefisien Muai Volume, γ ( /°C )
|
1.
|
Air
|
0,00021
|
2.
|
Alkohol (etil)
|
0,0011
|
3.
|
Alkohol ( metil )
|
0,0012
|
4.
|
Aseton
|
0,0015
|
5.
|
Gliserin
|
0,005
|
6.
|
Minyak Parafin
|
0,009
|
7.
|
Raksa
|
0,00018
|
Dengan mengetahui sifat dari zat cair, kita lebih mudah menentukan muai volume atau muai isi daripada muai panjang.
Koefisien muai volume ( γ ) adalah perbandingan antara perubahan volume ( ΔV ) dan volume mula-mula ( V₀ ) per satuan derajat celcius. Secara matematika dapat ditulis sebagai berikut.
ΔV
|
=
|
γ . Δt
|
V₀
| ||
V
|
=
|
V₀ ( 1 + γ . Δt )
|
Keterangan :
V = Volume akhir ( cmᶟ )
V₀ = Volume mula-mula ( cmᶟ )
ΔV = Pertambahan volume ( cmᶟ )
γ = Koefisien muai volume ( /°C )
Δt = Kenaikan suhu ( °C )
Dibawah ini akan diberikan contoh soal agar lebih mudah untuk dipahami.
Raksa pada suhu 0 °C volumenya 500 cmᶟ lalu dipanaskan sampai 60 °C. Bila koefisien muai ruang 0,00018 /°C. Hitunglah volume raksa setelah dipanaskan !
Penyelesaian :
Diketahui :
Vₒ = 500 cmᶟ
Δt = 60 °C - 0 °C = 60 °C
γ = 0,00018 /°C
Ditanya :
V =...?
Jawab :
V = V₀ ( 1 + γ . Δt )
V = 500 ( 1 + 0,00018 x 60 )
V = 500 ( 1,0108 )
V = 502,4 cmᶟ
Jadi, volume raksa setelah dipanaskan adalah 502,4 cmᶟ.
3) Pemuaian Zat Gas
Pernahkan kamu melihat balon udara? Balon udara dapat terbang menggunakan prinsip pemuaian pada zat gas. Pada saat udara dipanaskan, udara di dalam balon memuai.
Hal tersebut menyebabkan massa jenis udara yang berada di dalam balon berkurang sehingga menjadi lebih ringan daripada udara di sekitarnya. Kondisi ini mengakibatkan balon dapat mengudara dan mengangkat beban yang dibawanya.
Pemuaian yang terjadi pada zat gas sama halnya dengan pemuaian yang terjadi pada zat cair, yaitu hanya mengalami muai ruang saja. Pemuaian zat gas ini lebih besar daripada zat cair.
Untuk menghitung besarnya pemuaian volume gas dapat menggunakan persamaan berikut.
V = V₀ ( 1 + γ . Δt )
Keterangan:
V = Pertambahan volume ( mᶟ )
Vₒ = Volume mula-mula ( mᶟ )
γ = Koefisien muai volume ( °C⁻¹ )
Δt = Kenaikan suhu ( °C )
( Nilai γ sama untuk semua koefisien gas yaitu ( 1/273 °C⁻¹ = 0,00367 °C⁻¹).
Dibawah ini akan diberikan contoh soal agar lebih mudah untuk dipahami.
Suatu ruangan berisi 50 mᶟ udara pada suhu 25 °C. Berapakah volume udara dalam ruangan tersebut jika suhunya naik menjadi 40 °C ( koefisien muai volume udara adalah 0,00367 °C⁻¹ ) ?
Penyelesaian :
Diketahui :
Vₒ = 50 mᶟ
Δt = 40 °C – 25 °C = 15 °C
γ = 0,00367 °C⁻¹
Ditanya :
V =...?
Jawab :
V = V₀ ( 1 + γ . Δt )
V = 50 ( 1 + 0,00367 x 15 )
V = 52,7525 mᶟ
Jadi, volume udara setelah pemuaian adalah 52,7525 mᶟ
Pemuaian gas dibedakan menjadi 3 macam, yaitu :
(i) Pemuaian Gas pada Suhu Tetap ( isotermal )
Pemuaian gas pada suhu tetap berlaku hukum Boyle, yaitu :
“Gas di dalam ruang tertutup yang suhunya dijaga tetap, maka hasil kali tekanan dan volume gas adalah tetap.”
Dirumuskan sebagai berikut :
P V = tetap atau P1 V1 = P2 V2
Keterangan :
P = Tekanan gas ( atm )
V = Volume gas ( L )
Dibawah ini akan diberikan contoh soal agar lebih mudah untuk dipahami.
Suatu gas di dalam ruang tertutup memiliki tekanan 1 atm dan volume 4 L. Jika suhu gas dijaga tetap dan tekanan diubah menjadi 2 atm, berapakah volume gas ?
Penyelesaian :
Diketahui :
P1 = 1 atm
V1 = 4 L
P2 = 2 atm
Ditanya :
V2 = ...?
Jawab :
P1 V1 = P2 V2
1 atm x 4 L = 2 atm x V2
V2
|
=
|
1 atm
|
x 4 L
|
2 atm
|
V2 = 2 L
(ii) Pemuaian Gas pada Tekanan Tetap ( isobar )
Pemuaian gas pada tekanan tetap berlaku hukum Gay Lussac, yaitu :
“Gas di dalam ruang tertutup dengan tekanan dijaga tetap, maka volume gas sebanding dengan suhu mutlak gas.”
Dalam bentuk persamaan dapat dituliskan sebagai berikut :
V1
|
=
|
V2
|
T1
|
T2
|
Keterangan :
V = volume ( L )
T = suhu ( K )
Dibawah ini akan diberikan contoh soal agar lebih mudah untuk dipahami.
Suatu gas di dalam ruangan tertutup memiliki tekanan 1 atm, dengan suhu 27 °C, dan volume 2,4 L. Berapa volume gas tersebut pada suhu 127 °C jika mengalami proses pemuaian pada tekanan tetap ?
Penyelesaian :
Diketahui :
P = 1 atm
T1 = 27 °C = 300 °K
T2 = 127 °C = 400 °K
V1 = 2,4 L
Ditanya :
V2 = ...?
Jawab :
2,4 L
|
=
|
V2
|
300 °K
|
400 °K
|
2,4 L
|
=
|
V2
|
300 °K
|
400 °K
|
V2
|
=
|
2,4 L x 400 °K
|
300 °K
|
V2 = 3,2 L
(iii) Pemuaian Gas Pada Volume Tetap ( isokhorik )
Pemuaian gas pada volume tetap berlaku hukum Boyle-Gay Lussac, yaitu :
“Jika volume gas di dalam ruang tertutup dijaga tetap, maka tekanan gas sebanding dengan suhu mutlaknya.”
Hukum Boyle-Gay Lussac dirumuskan sebagai berikut :
P1 V1
|
=
|
P2 V2
|
T1
|
T2
|
Keterangan :
P = tekanan ( atm )
V = volume ( L )
T = suhu ( K )